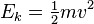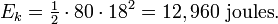250 below 10K internationally?

[Colonel Savage]

I was asking why it implies ATC can permit speeds in excess of 250 kts below 10,000 ft when operating in class A airspace. I didn't understand how you could be below 10,000 ft MSL AND in class A airspace...

It would be hard to do, considering that Class A is the old Positive Control Airspace from FL 180 to FL 600. Could it be a misprint in your GOM, like the reference to "10,000 knots" in the letter from "Rebecca" that started this thread? They do happen.

 

[AC560]

I was asking why it implies ATC can permit speeds in excess of 250 kts below 10,000 ft when operating in class A airspace. I didn't understand how you could be below 10,000 ft MSL AND in class A airspace.

Because many countries have class A airspace below 10,000 ft. Good portions of the UK for example are class A from 3,000 ft MSL on up.

 

[joe_pilot]

The short answer is Bird Strikes. Hitting a bird at 300 kts vs 250 kts will resule in 44% greater impact forces.

Where do you get those figures? Could be wrong here, but it sounds like a simple F=MA calculation. It should only be a 25% increase 300 vs 250 kts = 25% difference.

Again, maybe I'm missing something.

 

[Floatplane]

I wasn't asking what FOM meant (even though my current airline calls it a GOM).

I was asking why it implies ATC can permit speeds in excess of 250 kts below 10,000 ft when operating in class A airspace. I didn't understand how you could be below 10,000 ft MSL AND in class A airspace.

Another interesting item is that most FOMs and FARs only prohibit 250 kts below 10,000 MSL. So if I am landing at a high altitude airport, I wouldn't even be speed restricted until on short final. Seems like that violates the intent of the regulation.

I think you mean AGL not MSL! I hope you know the difference.

Many countries have Class A airspace below 10,000' MSL. However, I do not know of any in the U.S.

 

[Singlecoil]

Where do you get those figures? Could be wrong here, but it sounds like a simple F=MA calculation. It should only be a 25% increase 300 vs 250 kts = 25% difference.

Again, maybe I'm missing something.

I can't comment on the accuracy of the statistic, but kinetic energy increases with the square of velocity, not linearly as you suggest.

The 250 knots below ten rule came out of the Cerritos accident, didn't it? The one where the Cessna collided with the passenger jet over LA?

 

[Beetle007]

Many countries have Class A airspace below 10,000' MSL. However, I do not know of any in the U.S.

That was my original question. Can you name a location that has Class A airspace below 10,000?

Also for a different poster Force=Mass*Acceleration where acceleration units are (m/s)^2.

 

[Floatplane]

That was my original question. Can you name a location that has Class A airspace below 10,000?

Also for a different poster Force=Mass*Acceleration where acceleration units are (m/s)^2.

Try reading page 2 of this thread! LOL

 

[atpcliff]

Hi!

Why operationally over 250?
It also might be a small jet, that isn't safe to fly slow. The Air Force T-38 standard visual traffic pattern speed was 300 kts-VERY small wings and not much lift without LOTS of airflow.

I was at about 650 kts once, at about 4,000' or so, near Ft. Walton Beach (my instructor pointed out that it was probably a little fast-I had gotten so used to the high speeds that I hadn't noticed).

Why fly over 250?
I've had the controllers at least twice tell me to go faster. Once the guy screamed at me on the radio to increase my descent and not worry about my airspeed, and the other I was level at about 6,500', and the guy told me to "...speed 280 knots NOW".

I would guess both were probably traffic conflicts? I didn't argue or ask, I just did what they told me to.

A little more...
f=m*a (force = mass x acceleration). When you multiply, it does not "add up" linearly, it goes up, exponentially? Anyway, it goes up more than linearly.
Lets try it:
250 x 85,000 = 21,250,000
300 x 85,000 = 25,500,000
So, we increase the speed by 50 kts, or 20%.
The Energy increased by 4,250,000, or 20%???

Obviously, that math example sucked (I had one physics and chemistry class in HS, and one math class in college). I KNOW that force doesn't increase linearly.

Maybe someone here, who is better than I am at math/science can give us an accurate example/explaination!

cliff
GRB

 

[Singlecoil]

From wikipedia:

Kinetic energy of rigid bodies

In classical mechanics, the kinetic energy of a "point object" (a body so small that its size can be ignored), or a non-rotating rigid body, is given by the equation

where m is the mass and v is the speed of the body. In SI units (used for most modern scientific work), mass is measured in kilograms, speed in metres per second, and the resulting kinetic energy is in joules.
For example, one would calculate the kinetic energy of an 80 kg mass traveling at 18 meters per second (40 mph) as

Note that the kinetic energy increases with the square of the speed. This means, for example, that an object traveling twice as fast will have four times as much kinetic energy. As a result of this, a car traveling twice as fast requires four times as much distance to stop (assuming a constant braking force. See mechanical work).


So, for your example converted to kilograms and meters per second:
250 knots = 128.61 meters per second
300 knots = 154.33 meters per second
85,000 = 38555.35 kilograms


Ke for the 250 knot scenario is 318863002.15 joules
Ke for the 300 knot scenario is 459150822.53 joules


So for the 20% increase in speed, Ke increased about 44% which is not 40% probably due to rounding errors. ...or maybe it's the beer...

 

[filejw]

In many places in Europe "deleting the speed restriction below FL100" is standard practice. In fact, if you dont do and slow everyone else down you will get yelled at. This happens almost everytime I go to the UK.

Or AMS..

 

[ultrarunner]

The FAA abandoned this test when the NTSB was concerned about bird strikes...

Uhhh...when the heck did the FAA start giving a $hit what the NTSB thought!!!

When the heck did this change????

Someone PLEASE post the reference!!!!;-)

 

[bizjet800]

So for the 20% increase in speed, Ke increased about 44% which is not 40% probably due to rounding errors. ...or maybe it's the beer...

So what you are saying is if I drink 20% faster, I will get 44% drunker? Hummm

 

[WMUSIGPI]

I can't comment on the accuracy of the statistic, but kinetic energy increases with the square of velocity, not linearly as you suggest.

The 250 knots below ten rule came out of the Cerritos accident, didn't it? The one where the Cessna collided with the passenger jet over LA?

I think that was the one that created the TCA, what is now class B airspace. Before that all towered airports were basically what is today class D. Picture the fun of arriving in LAX or LGA if the airspace was just today's class D.......

 

[WMUSIGPI]

Quite simply, most airlines now restrict 250 kias below 10K in their FOM's or SOP's. I believe the reg's state you must comply with your companies FOM, SOP's, or the FAR's whichever is the most restrictive. Thus, 250 kias below 10K should be a non-topic unless your company does not specifically restrict it.

In my company's manual (Mesaba) it specifically states that when departing airports in Canada it is permitted to fly faster than 250kts on departure when cleared to climb above 10000ft. (per Canadian regs) I didn't remember seeing that in our manual before it was recently brought to my attention. (though I routinely did that in a Lear in a previous job and knew of the rule) It may have just been added with the CRJ's since the Avro's were limited to 250 below 8000ft anyways. But with the CRJ able to fly 330 below 8000ft it's now worth allowing us to do I guess. Either way it at least helped mentally on the Montreal COD's until Cleveland Center would slow us back to 250 approaching Aylmer VOR, UGH!!!.

 

[AMANSWORLD]

A birdstrike might hurt at 320kts. I've "heard" of people that do 340kts at 2000 ft when flying internationally. Probably not that fuel efficient either =)

Most jet a/c are certified Vmo/Mmo based on a birdstrike to the windshield. This is another reason for window heat and Vmo/Mmo changing speeds at various altitudes.

On another note "heavy" jets are allowed to fly whatever speed they need for manuvering in a specified configuration. The 250 thing is really an FAA deal also. Most countries in South America and east Europe as well as middle east have no clue what 250 is below 10000.